Articles by MSiA

|By Lingjun (Ivan) Chen and Nuo (Nora) Xu|

Problem Statement

Nowadays, personalized recommendation systems are implemented by many online businesses, which try to identify user’s specific tastes then provide them with relevant products to enhance user’s experience. Users, in turn, would be able to enjoy the convenience of exploring what they potentially like with ease and are often surprised by how good the recommended results are. However, mainstream restaurant recommendation apps have not adopted personalized restaurants recommenders generally. Therefore, finding an ideal restaurant is always a struggle for newcomers and sometimes even for local people, who are looking for places new and exciting to go. Inspired by such a challenge, we aim to build a personalized restaurant recommender system prototype that not only considers the interactions (visits) between customers and restaurants, but also incorporates metadata (side information) that expresses both the customer’s personal tastes and restaurants’ features. Such approach can increase each user’s experience of exploring and finding restaurants that are closer to their tastes. We used datasets provided by Yelp and a package named LightFM, which is a python library for recommendation engines to build our own restaurant recommender.

Here is an introductory article to refresh on some of the basic ideas and jargon on recommender systems before proceeding.

Github repository of LightFM: https://github.com/lyst/lightfm

Github repository for our model: https://github.com/Ivanclj/Yelp-Recommender

Background

When implementing recommender systems, researchers generally adopt two methods: Content-Based Filtering (CBF) and Collaborative Filtering (CF). CBF models users’ tastes based upon their past behaviors, but does not benefit from data on other users. On the contrary, CF looks at user/item interactions (visits) and tries to find similarities among users or items to do the recommender job. However, both methods have their limitations. A CBF-based system is limited by novelty in recommended results. Because it only looks at user’s past history, it never jumps to other areas that users might like but have not interacted with before. Additionally, if the quality of content does not contain enough information to discriminate the items precisely, CBF will perform poorly. On the other hand, CF suffers from sparse interaction matrix between users and items, where many users have very few interactions or even no interactions at all. This is also known as the cold start problem, which would be a huge problem especially for newcomers to certain areas to find suitable restaurants. To tackle this problem, we aim to develop a hybrid approach, which leverages both the collaborative information between users and items and user/item metadata to complete the recommendation job.

Dataset

We used three datasets in this project: business.json, review.json, and user.json. Dataset business contains geographical information about 192,609 businesses, categories and attributes, such as average star rating, hours, whether they offer parking and etc. Dataset review includes 6,685,900 review texts and ratings users write to businesses. Dataset user includes information like how long ago the user has joined Yelp, the number of reviews he/she has written, the number of specific compliments received, and his/her friend mapping on Yelp about 1,637,138 users. The three datasets can be merged by unique keys user_id and business_id. More detailed explanation of the data can be found in Yelp documentation (Source: https://www.yelp.com/dataset).

Data Cleaning & Feature Engineering

To build a hybrid recommender system, we would need an interaction matrix between users and items, metadata of restaurants that summarize their characteristics, and metadata associated with customers that indicate their taste preference.

Business dataset includes businesses of all categories from over 100 cities. For the reason that items (restaurants) in different cities have few interactions with each other, we filtered the dataset to keep only the city with the highest number of restaurants — Toronto (10,093 restaurants). Then we moved forward, exploring restaurant attributes that would potentially be useful in recommenders. Most features have many missing values across restaurants so we picked number of stars the restaurant was rated (0-5 scale), review counts of the restaurants, and the categories of the restaurants as item features. Usually each item (restaurant) has an average of 10 categories/tags assigned by Yelp, and there are 436 tags in total across all restaurants, such as seafood, vegetarian, breakfast & brunch, bars and so on. We decided to select top 60 tags with highest popularities since including some tags that only appear a few times out of more than 10k restaurants would add more noise in the recommender. Furthermore, we calculated TF-IDF (term frequency-inverse document frequency) values for each tag (Figure 2), which would be used as weights in model fitting later. We applied TF-IDF instead of binary value for the purpose of promoting core tags over incidental ones, and giving higher weight to tags that appear less frequently.

In review dataset, we found that there were cases where a unique user would rate one restaurant several times throughout his/her history. For such case, we only kept the most recent review since it reflected the user’s latest preference.

In order to remove user bias from subjective rating (some users rated a high score for every restaurant), we centered those users’ rating by subtracting their mean rating, and converted the results to 1 if positive and -1 if negative. The unrated items were kept as 0. The reasoning for this transformation is that we want to focus more on ranking the user liked restaurants and disliked restaurants in the correct order, rather than predicting user ratings on each restaurant, which would result in high variance over time.

The final step of data cleaning was to select out characteristics of users. We heuristically chose four features that are not sparse, which are number of reviews wrote, number of times reviews are regarded as useful, whether the user is active/elite in Yelp and most importantly, user’s favorite restaurant category from past interactions.

Evaluation Metric

In terms of the evaluation of recommenders, we decided to choose AUC (area under the curve) over RMSE (Root Mean Square Error) that was the most frequently used metric for measuring explicit recommendation system performance. RMSE emphasizes accuracy of rating prediction, which is how much customers like or dislike each recommended item. On the other hand, AUC is a decision-support metric that cares only whether customers like the item or not. In our case, figuring out customer preference in general is more important and practical than predicting their rating for each restaurant; therefore AUC is used in results evaluation below.

To explain the concept briefly, AUC is the area under the curve of ROC (receiver operating characteristic) that plots true positive rate against false positive rate with the increasing of recommendation set size. True positive rate (TPR) is the ratio of recommended items that users like to the total number of favored items, while false positive rate (FPR) is the ratio of recommended items that users dislike to the total number of unfavored items, as shown in Figure 3.

Additionally, we calculated precision at k scores for each user in the test set. Precision at k score measures the fraction of known positives in the first k positions of the recommended list. A perfect score is 1.0. We chose k = 5 in our setting but k could be any arbitrary number depends on how many items need to be shown at a time.

Methodology

1. Baseline Model

First off, we started with a baseline method. The underlying algorithm is to recommend items (restaurants) that are either popular or have high rating scores, regardless of features of items or feedback from the users. This method is useful for cold start (new customers) scenarios where limited information of the user or item is known. To implement the baseline model in Yelp data, we sorted restaurants by number of reviews and ratings in descending order, and then treated top k as a recommended list indiscriminately for all customers.

Figure 4 illustrates that AUC value of the plot above is very close to 0.5. This results infers that given a recommended restaurant, a random user has a 50% chance of liking it. Unsurprisingly, the baseline method performed poorly and therefore, a more sophisticated model is needed.

2. LightFM Model:

a. Matrix Factorization

LightFM incorporates matrix factorization model, which decomposes the interaction matrix into two matrices (user and item), such that when you multiply them you retain the original interaction matrix. Figure 5 illustrates this notion graphically. The factorized matrices are known as user and item embeddings,  which have the same number or rows (latent vector dimension) but different number of columns depending on the size of the users or items.

The latent embeddings could capture latent features about attributes of users and items, which represent their tastes. For example, people who like Asian restaurants would have similar embeddings with those that prefer Chinese restaurants but are probably further away from those that are fond of Mexican food in the vector space. An embedding is estimated for every feature, and embeddings across all features sum up to arrive at representations for users and items. Figure 6 shows the formula of how features are summed.

b. Loss Function

LightFM implements four loss functions for different scenarios. They are logistic loss, BPR (Bayesian Personalized Ranking pairwise loss), WARP (Weighted Approximate-Rank pairwise loss) and k-OS WARP, which are all well documented in the LightFM package.

BPR and WARP are special loss functions that belong to a method named Learning to Rank and are originated from information retrieval theory. The main idea of BPR is sampling positive and negative items, then running pairwise comparisons. It first selects a user u and then a random item i which user u views as positive. Then it randomly selects an item j which user u views as negative. After it has both samples, it calculates the predicted score for both items by calculating the dot product of the user and item factorized matrices. Next, it calculates the difference between two predicted scores and then passes this difference through a sigmoid function and uses it as a weighting to update all of the model parameters via stochastic gradient descent. In this way, we completely disregarded how well we predict the rating for each user-item pair and focused only on the relative ranking between items for a user instead.

WARP works in similar fashion as it deals with triplet loss (user, positive item, negative item) like BPR. However, unlike BPR that updates parameters for every iteration, WARP only updates parameters when the model predicts the negative item has a higher score than the positive item. If not, WARP keeps on drawing negative samples until it finds a rank violation or hits some threshold for trying. Besides, WARP makes a larger gradient update if a violating negative example is found at the first try, which indicates that many negative items are ranked higher than positives items given the current state of the model. Or WARP makes a smaller update if it takes many sampling to find a violating example, which infers the model is likely to be close to the optimum and should be updated at a low rate.

Generally, WARP performs a lot better than BPR. However, WARP takes more time to train since if the rank is not violated, it keeps on sampling negative samples until a violation happens. Moreover, as more epochs (iterations) are trained, WARP becomes slower as we can seen in Figure 7. This phenomenon is because a violation becomes more difficult to find. Thus, setting a cutoff value for searching is essential for training with WARP loss.

We compared models across logistic, BRR and WARP to find the best loss for our models.

c. Model Establishment

i. Pure Collaborative Filtering

Pure CF model is achieved by LightFM if only passes in the interaction matrix to fit the model. This ensures that the model has access only to the interaction information but no other metadata information. We split the data into train and test, with 20% interactions (82,127) in test and 80% (328,507) interactions in train and checked that the two sets were fully disjointed. Next, we initialized random parameters to fit the model using three different losses (logistic, BPR, WARP). However, since our parameters are randomly chosen, it was necessary to perform hyperparameters search to obtain the best model. To do that, we utilized the scikit-optimizer package to search through a range of values for different hyperparameters and evaluated them on mean AUC score. Outputs are shown in Figure 8 and Figure 9.

ii. Hybrid Matrix Factorization

At this stage, we were fitting the hybrid model that not only takes in interaction matrix, but also item features and user features as well.

Item features is a matrix with dimension 10093 x 10156, which is the number of items times number of item features. The number of item features equals to 10156 for the reason that LightFM internally creates a unique feature for each item in addition to other features. So 10156 = 10093 (unique feature) + restaurant stars + review count + 61 tags. Since LightFM normalizes each row in the item features to have its sum to 1, some of the features such as review count, which have very large values, could potentially dominate the weight assigned. To account for that, we normalized some features with large values by taking the log value and then dividing by their max. The same procedure was applied to build the user features matrix (92,381 x 92,420). We also added user alpha and item alpha into the model as regularization parameters to control overfitting. Hyperparameter search for the hybrid model was then performed. Outputs are shown in Figure 10 and Figure 11.

Result

1. Model Evaluation

a. AUC score

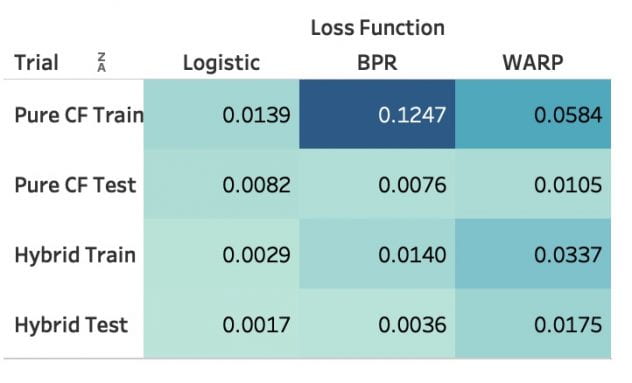
Figure 12 shows the results of mean AUC score across all users in a test set of the models with different losses and trials. These results are based upon optimal hyperparameters for each model through scikit-optimizer library, which performs cross-validation to find the best set of parameters. Multiple trials were run to account for random noises.

As we can see, WARP performs best both in a pure CF setting as well as a hybrid setting. Logistic loss seems to perform worse when metadata is included while all learning to rank method performs better in a hybrid setting. BPR seems to fit the training set very well but performs poorly when generalized to the test set, indicating a problem with overfitting even after tuning for optimal parameters.

b. Precision at 5

Figure 13 shows the results of mean precision at 5 score across all users in the test set of the models with different losses and trials right after calculating AUC so they are from the same model within each setting. Precision at 5 score has similar results with AUC where WARP performs best out of three losses. The number are relatively low since most users in the test set has a few interactions (cold start users), so most top 5 recommended items by the model are the ones that they have not interacted with, which resulted in very low precision overall. Since our goal was to optimize AUC, we focused on making sure positive items were placed before negative but the order of positive items with interactions were not necessarily placed in front. So we should only compare the relative difference between these scores instead of their magnitude.

2. Recommendation Demo

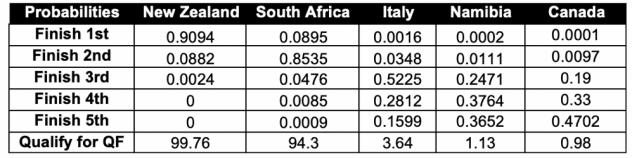
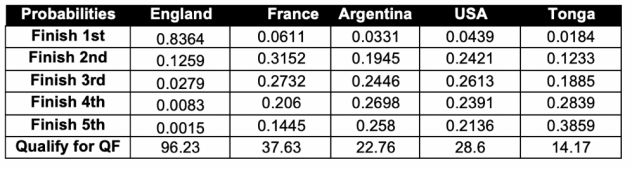
Figure 14 and Figure 15 are demos for recommendation on random users. “Known positives” are restaurants that the specific user went to and had positive interactions with. “Recommended” are the top k (k = 5 in this case) restaurants recommended for this user.

Figure 14 demonstrates a classical cold start case where user 66 has only one positive interaction but we are trying to recommend 5 to him/her. So precision would be low but we can see Japanese and Thai restaurants are recommended as it is close to the known positive, which this user had interaction with. There are also Ice cream and Brunch places recommended, which we suspect is either from the collaborative information or other metadata such as stars and review counts of the restaurant. For user 74, out of 5 recommended results, the user had positive interaction with 2 of them so the precision at 5 = ⅖ = 0.4, as shown in Figure 15.

The sample recommendation function is a particularly useful tool because it lets you do some eye tests on the recommendation results. In this case, we printed out the categories of restaurants to compare, but one can also print out restaurant stars or review counts to see if it makes more sense.

3. Tag Similarity

Another great feature from LightFM is that the estimated item embeddings can actually capture the semantic characteristics of the tags. Instead of driving by textual corpus coincidence statistics like word2vec does, the way LightFM finds similar tags is purely based on interaction data. These features are useful in terms of applying collaborative tagging for new restaurants, group tags into bigger categories, and providing justification for the recommender system. From Figure 16, we can see that most tags recommended share semantic similarity with target tags indeed.

Conclusion & Next Step

In this paper, we explored the potentials of adopting a hybrid approach to build a personalized restaurant recommender system using Yelp’s dataset and LightFM package. We also compared its performance with a pure collaborative filtering model and with different loss functions implemented in the packages. In addition to just basic interaction information between items and users in pure collaborative filtering, the hybrid recommendation system also utilizes item & user metadata, which makes it perform better in the learning-to-rank setting (as shown above) and more robust to cold-start problems.

As for next step, it will be easy to quickly expand the scope of our project to include more cities into the recommender system. For now our recommender aims only at users in Toronto, but it could be applied to all locations if needed as long as information on users and items are available. Considering further optimizing of the system, we suggest including more features, such as demographic data of users and geohash of restaurants, with the hope that more variation could be explained. In addition, manipulating the tags of items for higher inclusiveness and lower overlapping could be useful in terms of both matching customers with similar tastes and dealing with computational cost.

---

1. Agrawal, A. (2018, June 13). Solving business usecases by recommender system using lightFM. Retrieved from https://towardsdatascience.com/solving-business-usecases-by-recommender-system-using-lightfm-4ba7b3ac8e62
2. Kula, M. (2015). Metadata embeddings for user and item cold-start recommendations. arXiv preprint arXiv:1507.08439.
3. Rendle, S., Freudenthaler, C., Gantner, Z., & Schmidt-Thieme, L. (2009, June). BPR: Bayesian personalized ranking from implicit feedback. In Proceedings of the twenty-fifth conference on uncertainty in artificial intelligence (pp. 452-461). AUAI Press.
4. Rosenthal, E. (2016, November 7). Learning to rank Sketchfab models with LightFM. Retrieved from https://www.ethanrosenthal.com/2016/11/07/implicit-mf-part-2/
5. Schröder, G., Thiele, M., & Lehner, W. (2011, October). Setting goals and choosing metrics for recommender system evaluations. In CEUR Workshop Proc (Vol. 811, pp. 78-85).
6. Weston, J., Bengio, S., & Usunier, N. (2011, June). Wsabie: Scaling up to large vocabulary image annotation. In Twenty-Second International Joint Conference on Artificial Intelligence.

|By Marcus Thuillier|

ELOR Rating System

Introduction

Ever since I was little, rugby has been my favorite sport. Rugby is still a developing sport in the USA, but the national team has been in every World Cup, but one and is now solidly entrenched as a top 15 team in the world. Rugby rules and scoring are similar to American Football’s, and some players even switch between the two (Nate Ebner, for example, was both an NFL player for the Patriots and a rugby player for the USA Rugby 7’s team). Something I was always fascinated with was how much of an NFL game was quantifiable with stats. You could get favorites, pre-game odds, in-game odds, etc. World Rugby rankings could not do that (except for giving you the ranking from 0 to 100 before the game), and it left me wanting for a more comprehensive ranking system that could be used in more dynamic ways. For example, on October 6th, 2018, New Zealand (the number one team in the world) came back from 17 points down to beat South Africa in just 20 minutes of playing time. In the world of Rugby Union, this kind of result is rare. I was eager for a way to quantify just how surprising this result was. Since the world rugby ranking system has never been used in order to do this, I settled on the ELO rating system, which allows, amongst other things, for in-game win probability adjustments and would be good to evaluate how daunting this comeback really was. Let’s dive right into it.

Background

Dr. Arpad Elo developed ELO in the 1950s to rank chess players. Since then, ELO has most notably been adapted to the National Basketball Association and National Football League by the journalists of the website FiveThirtyEight. A version for world soccer also exists on eloratings.net. I will be looking to develop an ELO Rating for Rugby (ELO-Rugby, or ELOR) and will use NFL ELO Ratings as a reference, for a couple of reasons: a) Rugby Union and American football scoring is relatively similar: seven points for a touchdown / converted try, three points for a field goal / penalty kick (this makes it easier when building the model to look at margin of victory for example and helps in determining a conversion between points and ELO score) and b) NFL teams play between 16 and 19 (if they go all the way to the Super Bowl) games per season, and most major rugby union teams participate in between 10 and 15 games per season. The similarities make the NFL ELO system a good starting point, but some tweaks and changes need to be implemented.

The ELOR Rating: Theory

The ELOR rating will take into account all game results since the year 1890 for rugby, available via the website stats.espnscrum.com. This start date was selected because that is the earliest for which we have game results with modern point scoring. Once all these games are accounted for, the ELOR Rating will be calculated as follows:

R’ is the new Rating

R_old is the old Rating

ELO_old and  ELO_away are the home and away ELOR ratings.

corr_coeff is the “auto correlation adjustment multiplier” used to deal with autocorrelation.

margin_coeff is the margin coefficient. If only the margin were used, games between the top team New Zealand and a team like Portugal would weigh way too heavily into the rating. With this coefficient, those big blowouts are capped in their weight based on a logarithmic scale.

Those two coefficients could use some tinkering when developing the model further. For now, though, the two coefficients will be the same as those used by FiveThirtyEight for their NFL model. Those values are:

W is 1 for a home win, .5 for a draw and 0 for a home loss. Those values are used in most ELO models, and they allow you to compare the actual result with the predicted result, which is a probability between 0 and 1.

In W_*, the Win Expectancy, the diff is calculated by the difference in rating plus a home field advantage constant.

The Brier Score is commonly used to measure the accuracy of binary probabilistic forecasts, in fields like meteorology and recently in sports analytics. I used the Brier Score to optimize the model and determine the K factor and home-field advantage. The Brier Score is calculated as follows:

The lower the Brier Score, the better the accuracy of the ELOR model.

The Home Field advantage (x-axis) has been optimized for the model, in conjunction with the K-Factor (five different colors for 10, 20, 30, 40 and 50) in the following two graphs. The Brier Score is on the y-axis. After finding that values around K=40 had the lowest Brier Score across the board (Figure 4), I focused on just those values in Figure 5.

Following these tests, I chose to go with a home advantage of 75 ELO points and a relatively high K coefficient value of 40 (which gave the lowest Brier Score), leading to a quicker response from the model to the new game result.

Limitations of my ELOR

Several limitations I noticed or notes I made when building my ELOR model:

1. The top 10 teams in the world, the so-called Tier I teams, have ruled World Rugby since it turned professional in 1995: they have better infrastructures, more regular matches, compete in the two Tier I tournaments each year and are present in almost all semi-finals and quarterfinals of World Cups. Those teams are in no specific order: New Zealand, Australia, and South Africa in the Southern Hemisphere (the founding members of the Tri-Nations in 1996), France, England, Scotland, Wales, Ireland in the Northern Hemisphere (who disputed the Five Nations up until 1999). Argentina and Italy were added, as they regularly play these teams in the now Rugby Championship (which followed the Tri-Nations) and Six Nations (which followed the Five Nations). It is hard to compensate for the fact that there is little to no interaction between teams in Tier I and all the other teams outside of World Cups. In further iterations of the models, a way to account for some of the model’s overestimation of highly successful Tier II teams (any of Georgia, Portugal, Romania, Russia, Spain, Canada, USA, Uruguay, Namibia, Japan, Fiji, Samoa and Tonga) that barely play against Tier I teams could be implemented. An option I am considering for a further iteration of the model that I want to develop before next year’s World Cup is to weigh down the rankings of Tier II nations when they play Tier I nations, but for now, it will not be changed.

2. Some teams do not play much, especially before the 2000s. For the Tier I teams, they usually play 4 or 6 games in the Six Nations (Northern Hemisphere), and Rugby Championship (Southern Hemisphere), 3 or 4 games in the June international matches and 3 or 4 matches in the November matches. Most teams play less than that or play games at less than full strength (due to conflicting club schedules for teams like Fiji and Tonga for example). This means that some teams will have high volatility in their rankings, something the ELOR has issues with as it is perfected with increased sample size. That is a significant difference with the models for the NBA and NFL, where each team plays the same amount of games each season (excepting playoffs) and have all their players available during the season (barring injuries). This is further aggravated by the fact that some data for some games appear to be missing from the dataset and is difficult to account for.

3. Teams like Argentina sometimes field a B team to their national team. For Argentina, that team is Argentina A or Argentina XV, and they mostly compete against teams in the Americas Rugby Championship and Nations Cup. The Argentina A team is made up mostly of players from the local club league (as opposed to pro players in the Argentina team who play in the Super Rugby, the club championship for the Southern Hemisphere teams) and is still written as “Argentina” in the dataset, which would help teams like Uruguay, the USA or Georgia in case of victory against that “Tier I” team. It could be considered in future iterations of the model to differentiate A and B teams, but it is difficult to check team compositions for each match to determine that.

Those three issues will come up in the ELOR ranking. The ELOR could be updated in further iterations to correct for those three issues. I have tried to address them in the way I calculated the ELOR, like with the balancing of missing games in the dataset by higher K-factor, but especially for volatility with Tier II teams and Tier III teams (all others), it is just a factor that is inherent to world rugby that has to be kept in mind when looking at the rankings.

Implementing ELOR

The ELOR is established in a series of python codes, with visualizations done in both R and Tableau. The Python code first scraps the data from the ESPN website using BeautifulSoup. The ELOR then is initialized, 1500 for all teams. A following code is then used to update the ELOR based on each game result and according to the original ELO formula mentioned above. Finally, a final code is used to analyze the results of the ELOR predictions.

Results

For comparisons, here are the top 25 teams in World Rugby rankings and ELOR ratings as of November 26, 2018.

A few observations: Fiji, after beating tier I team France during November’s international
matches, jumps to eighth both in the world ranking and the ELOR rankings. The first surprise comes from the USA’s place at number 10 in the ELOR ranking (12th per Rugby World), but it has to be considered that they had an excellent 2018 year, losing only against Ireland and the Maori All Blacks, and beating Scotland and Argentina XV (which counts as “Argentina” in the dataset) this season. The second surprise is that Italy, despite a convincing victory over Georgia in the November international matches, barely appears in ELOR’s top 15 after consistently playing and losing to better Tier I teams (notably not winning any games in the Six Nations in the past three years). This is however in line with World Rugby Rankings.

Otherwise, the rankings are fairly consistent (although past position fifteen, most teams have a star indicating a difference between the two rankings, but they are mostly within one or two positions of difference). The ELOR was also an improvement over world rugby rankings as it had all 20 teams qualified for next year’s World Cup in its top 21 teams (highlighted in red), the other team being Romania (who originally qualified but got sanctioned for fielding ineligible players) at 19. Canada, the last team to qualify for the World Cup, shows up at 21 in the ELOR ranking. World rugby’s ranking has the last qualified team for the World Cup, Namibia, at 22 in its ranking.

The ELOR Ranking provides another significant improvement over the World Rugby Ranking. Where the World Rugby Rankings published its first edition in September of 2003, in time for the 2003 Rugby World Cup, the ELOR Ranking is updated since the first game played in 1890. Now, the ELOR needs teams to play many games to improve accuracy and so the earliest ratings will probably not be too accurate. However, one can expect the ELOR to be a reliable ranking system for teams as soon as they reach upwards of 20 to 30 international test matches played. The ranking will always be more accurate in recent years, as teams play more matches and have over 100 years of history that is taken into account, but ELOR realistically allows for Rugby Rankings to be calculated as far back as the early 20th century, which is a sizeable improvement over the World Rugby Rankings that has only been in place for the past 15 years. This is implemented in an R code that demands user input for a date and outputs the ELOR ranking at that date in time, all the way back to 1890.

On top of creating rankings, ELORs huge advantage is that it allows for pregame and in-game predictions. The pregame win probability is based on the probability formula mentioned in the “The ELOR Rating: Theory” part (calculation of Win Expectancy). The in-game prediction is calculated as follows:

After running ELOR, the following tables for pregame predictions were output:

As I inched closer to the conclusion of this project, I only needed one thing to determine in-game probabilities. I needed bookmaker odds for the games. However, gambling on international rugby is not very widespread, so I lacked in sample size. I used some of the lines I could find and matched them up with the pregame ELO rating difference between the teams. I then fit a quadratic equation for best fit, but it is a very loose estimate. Interpret the point-spread predictions as a simple estimate of winning margin, that loosely fits bookmaker odds. It can be used to determine in-game probabilities for now and will be refined further when I can find more odds or with the help of historical data. In the next iteration of the ELOR model, I will look at historical results and margins of victories to determine a better equation to find game odds. For now, however, the results are interpreted based on the following equation:

75 ELO points, which corresponds to the home field advantage, procures about a 5.75-points boost based on historical data (average margin of victory for home teams since 1890) and is added as another data point to find the best-fit equation.

Now that I have all the elements, I can circle back to the question that prompted the development of ELOR in the first place: How clutch had the All Blacks been in that game against South Africa? In the aforementioned game, they were down 30-13, away from home in South Africa, with 18 minutes to go. We can find the pregame probabilities from the above table.

New Zealand came in as an 88.2% favorite (about 430 points difference between their ELOR and South Africa’s ELOR), according to the ELOR. We can also estimate the initial margin (about 15.5 points) and calculate in-game probabilities. This is what happened:

With 19 minutes to go, South Africa was about a 75% favorite to win the game. Jumping to 5 minutes remaining, up 30-18, South Africa was an overwhelming favorite at 96.8%. This means that if this game was played 1,000 times and the score was 30-18 at the 75th minute, South Africa would win 968 of those games and New Zealand only 32. And this was one of those 32 games. With 5 minutes left, New Zealand’s odds were only of 31.25/1.

Coming back to the original question: Was that New Zealand team clutch in that game? And the answer is pretty straightforward. New Zealand was very clutch, coming back from 1000/32 odds to win the game. And in the end, the game ended as predicted by ELOR, with a New Zealand victory.

To test the ELOR, I used November’s 22 international matches. I once again used the Brier
Score to evaluate the skill of ELOR’s forecasting. I chose to compare the ELOR with the ranking system from rugbypass.com over the course of the November test matches. RugbyPass developed a Rugby Index (RI), which they use to rank individual players based on their action in games and is updated after each game. This allows them to compute the player’s shape in both club and international rugby. It is based on an adaptation of the ELO model and has been modified with human input and other algorithms. After computing the players’ score, a team score is established, which they then use to determine win probabilities.

Those are the probabilities I will test my model against. A couple of things on the Rugby Index: the Rugby Index for a team depends on the lineup, so it will take into account injuries, which my ELOR does not. If, say, a middling team misses their best player, the Rugby Index will probably be better equipped to adjust the Win % odds than my ELOR. The second element however is that since it tracks players in the top rugby leagues around the world on the club level to develop its rating, the Rugby Index only has 18 international team (with players who play in top club leagues) in its repertoire. My ELOR Rating, on the other hand, has tracked every team that has played at least one game since 1890. Where the ELOR rating lacks in predicting unusual events (a top player being injured for example), it has more depth than the Rugby Index at the international level (ratings for more teams past Canada).

The following table and the Brier Scores were computed for 22 games in November (winner in Bold):

Over 22 games, ELOR predicted 18 out of 22 games correctly (over 80%), while the Rugby Index predicted just one more correctly. The four games ELOR missed were:

1. Italy v Georgia, a Tier 1 / Tier 2 matchup. Georgia was a favorite, but Italy held on for a comfortable victory.

2. Scotland v South Africa. Favorite Scotland lost at home to underdog South Africa. The RI also predicted that one wrong.

3. Ireland v New Zealand. The first matchup between number 1 and number 2 in the world in a long time, New Zealand had a scare the week before against England and Ireland thoroughly dominated.

4. France v Fiji, another Tier 1 / Tier 2 matchup. Favorite France lost the game and its place in the top 8 of world rugby against the elite Tier 2 nation, Fiji. The RI also predicted that one wrong.

After all those games, ELOR was able to react and adjust, as Italy and Ireland closed the gap on Georgia and New Zealand and South Africa, and Fiji leaped Scotland and France respectively.

The ELOR model achieved a Brier Score of .113, and the Rugby Index achieved a Brier Score of .104.

The Rugby Index performed a little bit better, which is to be expected seeing as they have more “up-to-date” ratings that consider player forms and injuries. However, the ELOR rating still predicted almost 82% of the games correctly, up from 70% on the entire dataset and up from 71% for games where at least one Tier I team plays in the entire dataset.

The Brier Score also showed an improvement with .113, down from 0.19 on the entire dataset and down from 0.136 for games where at least one Tier I team plays in the entire dataset. Finally, although the Rugby Index might be slightly more accurate when it comes to the top teams, the ELOR rating I created provides information on many more teams and many more matches than the Rugby Index. The Rugby Index, for example, has no information on Namibia, one of 20 teams in next year’s World Cup. The ELOR rating has that information and could be used to calculate World Cup odds (see Appendix I).

¹ http://www.footballperspective.com/the-biggest-quarter-by-quarter-comebacks-since-1978/

Conclusion

I was delighted by this first iteration of the ELOR. It is able to answer questions about in-game probabilities like “down 13 points with 15 minutes to go, what are New Zealand’s chances to win a game against Australia?”. ELOR holds its own in prediction capabilities and ability to quickly adjust its ratings and rankings based on recent results, providing a viable alternative to the World Rugby Ranking. It also allows establishing rankings for the earlier times of rugby, when the World Rugby Ranking did not exist. Furthermore, it is a tremendous tool when it comes to predicting tournaments, where it can be used in a Monte Carlo simulation (see Appendix I). It even performs better than forecasting models in other sports like basketball (see Appendix II). There are improvements to be made, however. I can look at developing an “autocorrelation adjustment multiplier” and margin coefficient myself, instead of using the ones FiveThirtyEight developed for the NFL. I could also look at weighing Tier I vs. Tier II matchups differently, which would probably help a team like Italy, who wins almost all their games against Tier II teams but loses almost all against Tier I teams, in the rankings. Another step would be to look for a complete dataset, or weigh World Cup games differently as they give us a rare opportunity to see Tier I and Tier II nations playing each other. For now, the first edition of the ELOR has performed better than I could have expected at the beginning of this project, and its accuracy will continue to improve as more games are added to the database. It will also be used to forecast next year’s Six Nations, hopefully improving on November’s 80% accuracy performance. ELOR is a viable, flexible and complete rating system for Rugby Union, one that has shown it is already up to par with other rugby union rankings systems and will only be ameliorated in future iterations.

Appendix

I. Forecasting the 2019 World Cup with a Monte Carlo simulation

I used a Monte Carlo simulation to simulate 10,000 World Cup results, and these are the results (Teams in the World Cup get a bonus point for scoring 4+ tries or losing by less than 7 points, but this simulation only accounted for wins and losses). I have used the ELOR ratings as of November 27, 2018.

Average wins for teams in a group will add up to 10 (with some rounding error) and the percentage chance of qualifying for the quarterfinal will add up to 200% since there are two spots for each group (top two teams). Thus:

With the Monte Carlo with 10,000 simulations, Ireland got 3.83 wins on average, Scotland 2.77, Japan 1.95, Russia .77 and Samoa .68.

With the Monte Carlo with 10,000 simulations, New Zealand got 3.9 wins on average, South Africa 3, Italy 1.43, Namibia .92 and Canada .75.

With the Monte Carlo with 10,000 simulations, England got 3.67 wins on average, France 1.93, Argentina 1.52, USA 1.68 and Tonga 1.2.

With the Monte Carlo with 10,000 simulations, Australia got 2.65 wins on average, Wales 3.61, Georgia 1.22, Fiji 2 and Uruguay .52.

As expected from their ELOR ratings, New Zealand and Ireland are the two overwhelming favorites for the World Cup. Only six teams, Wales, England, Scotland and Australia on top of the two mentioned before have over a 1% chance of winning the World Cup according to the model (with South Africa having a .99% chance). The likely semifinals are Ireland-Wales and New Zealand-England, a dramatic shift from four years ago when all four Southern teams (New Zealand, Australia, South Africa and Argentina) were the semi-finalists. Things can and will change, especially after the Six Nations of 2019 and some of the preparation games over the summer, but ten months away from the World Cup, the ELOR predicts a New Zealand win over Ireland, with the previously mentioned semi-finals in play. Finally, the most likely quarter-finals would be Ireland-South Africa, New Zealand-Scotland, England-Australia and Wales-France, leaving traditional heavyweight Argentina and underdog Fiji (who has the highest odds of advancing to the quarter-finals of any Tier II nation, close to 30%) watching from home.

II. Performance of the model vs. models in other sports

In evaluating the performance of my model, I looked for the performance of forecasting models in different sports. Once again using the Brier Score as a comparator, I found a blog post on “inpredictable² ”, comparing their predictive model with ESPN’s NBA model, which came up with the following result:

At the beginning of the game, when the model forecasts win probabilities for teams, Inpredictable obtained a Brier Score of .215 and ESPN had a score of .197. The ELOR rating I have worked on and developed achieves a Brier Score of 0.19 at the beginning of the game, which is better than both the aforementioned models. This was a good indication of the performance of the ELOR model for world rugby, as evidenced by the lower Brier Score value obtained when predicting match winners compared to forecasting methods in other sports.

² http://www.inpredictable.com/2018/01/judging-win-probability-models.html#more

Acknowledgments

I wanted to acknowledge Eta Cohort classmate Ted Carlson’s help in directing me towards the Brier Score as a valuable estimate of my forecasting model’s accuracy. I also wanted to thank my parents who share my love of rugby and advised and supported me in the building and testing of this model.

| By Ethel Shiqi Zhang |

As students in the Master of Science in Analytics (MSiA) Program, we are given a plethora of opportunities to engage with clients to apply our newly-minted analytics skills by tackling real-world problems.

This year, a group of four students paired up with IBM Analytics to carry out a project with Chicago Botanic Garden (the Garden). As the spring quarter ended, we also wrapped up this five-month long project with the Garden. The project really had it all — there was laughter, confusion, challenges, and midnight munchies. Here is a recap of this wonderful project with the Garden from my perspective. I hope it will help you gain some insights into the student life at MSiA and how we practice Data Science in real life to make impacts.

To guide your journey through this memoir, I’ve broken it down into four parts.

1. Client Overview
2. Project Mission
3. Data Analytics in Practice
4. Lessons Learned & Next Steps

Now that you are equipped with the map to this journey, let’s get started!

I. Client Overview

The Chicago Botanic Garden (the Garden) came into existence more than 40 years ago (1965), and it aims to be Urbs in Horto, meaning “city in a garden”.  In 2017, more than one million people visited the Garden’s 27 gardens and four natural areas.

The Garden has around 50,000 members as of 2017, making its membership base one of the largest of any U.S. botanic garden. Members of various ages, interests, and background participate in programs, take classes, and stroll the grounds year-round. At times, these members make donations to assist the Garden with achieving its mission.

II. Project Mission

With such a large membership base, the Garden is interested in leveraging a systematic analytical approach to derive some effective ways to engage its members and reinforce their connections with the garden.

With this goal in mind, the project team divided the project into two phases. Phase I focuses on exploratory data analysis which allows the Garden to understand the overall portfolio of its members. Phase II focuses on discovering the natural groupings of the members in order to target efforts towards donors who donate in different patterns.

III. Data Analytics in Practice

Phase I: Exploratory Data Analysis

The exploratory data analysis phase is when a lot of the data cleaning and Tableau charting happened. As we got more familiar with the data, we found some interesting insights which guided us in our feature selection for the next phase.

One of the thought-provoking insights in the first phase was the manifestation of the 80/20 rule. We discovered that less than 10% of the members donated over 80% of total donation to the Garden.

As a result, when studying donation behavior, we were really looking at a small sample size and searching among the 50k members for the ones who were most likely to donate.

Phase II: Clustering

To systematically identify the members who felt strong connections with the Garden (manifested in donations in this case), we carried out a clustering exercise. The methodology of our clustering can be broken down into this 6-step process and summarized in this beautiful graph made by one of my teammates:

1. Feature Selection
2. Data Preprocessing
3. Dimension Reduction (Principal Component Analysis)
4. Multiple methods clustering
5. Clustering results evaluation
6. Clusters formation & interpretation

Following these steps, we identified 6 clusters for the 50k members of the Garden. The distribution of the clusters mirrors the distribution of the donation amount that we have seen earlier: only a small percentage of the members are identified as high potential donors.

Once we finalized the clusters, we performed more exploratory data analysis to profile the clusters:

To understand what makes each cluster different, we studied the underlying differences between clusters. Several attributes out of the 70+ attributes we selected explained the differences the most. Some of these attributes include distance to park and historical park events attendance.

To understand why people in the same cluster still have diverging donation behaviors, we studied the difference within clusters between donors and non-donors.  Several attributes seems to contribute most to the within clusters differences. One of such attributes is event attendance. In most cases, the donors participate more in park events than the non-donors.

Data Driven Recommendations

Discoveries like this gave us the foundation to design a targeted relationship management strategy for the Garden. For example, in the case of event engagement, a reasonable strategy is to engage the Park Lovers who have not been donating (Park Lovers non-donors) to attend more featured and seasonal events in the hope of bringing their engagement with the park to the level of their fellow Park Loving donors.

With analysis like this, we were able to advise the Garden to customize its engagement strategy in a more effective fashion.

P.S. If you are wondering what a featured / seasonal event is like, here is a picture from the Orchid Show at the Garden, a seasonal event hosted in March 2018.

IV. Lesson Learned & Next Steps

It has been a great journey working with the Garden and IBM. I was excited to apply the data science skills I learned in school to real life problems and hopefully make an impact.

I have learned so much working with this brilliant team. In terms of my biggest take-away, instead of repeating the cliché that data is messy and arguing for what the best clustering model is (the answer by the way is almost always “it depends”), I want to focus on one message that I took home from this project: your model only matters when it can make an impact.

No matter how good your model is on paper (e.g. low BIC score or high silhouette score), it doesn’t matter until it can make an impact. That can mean that your clustering result should be interpretable or that it is actionable. Even the definition of impact will differ from case to case. The point is, as much as you should let your data guide you to discoveries, you should also not lose sight of why you came to the data in the first place.

So, I’m interested to see how our recommendations for the Garden will work out in the near future.

Before then, I hope that the memoir of my journey on the Garden’s project make an impact on demystifying the application of data science in real-world business problems.

---

Acknowledgements: This project has been carried out by four MSiA students and is supported by both the Garden and IBM. The project team in figure 7: (left to right) Gwen Vanderburg (Garden), Jamie Chen (MSiA), Michael Gao (MSiA), Ethel Zhang (MSiA), Ahsan Rehman (IBM, MSiA alumnus), Andrew Warzecha (IBM), Jane Chu (IBM), and Carolynn Kotlarski (Garden).