09/21: Wouter van Limbeek
Commensurators and arithmeticity of thin groups
Abstract: The commensurator of a discrete, Zariski-dense subgroup 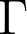 of a simple Lie group
of a simple Lie group 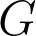 contains information on the arithmetic nature of
contains information on the arithmetic nature of 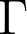 : For example, in 1974, Margulis proved that if
: For example, in 1974, Margulis proved that if 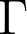 is a lattice and its commensurator is dense, then
is a lattice and its commensurator is dense, then 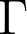 is arithmetic. In 2011, Shalom asked if the same is true only assuming
is arithmetic. In 2011, Shalom asked if the same is true only assuming 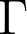 is Zariski-dense in
is Zariski-dense in 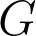 . I will report on recent progress on this question that uses ideas from infinite ergodic theory, profinite actions, representation theory, Brownian motion, random walks and the structure of locally compact groups. I will show how these combine to give information on commensurators and applications to problems in group theory, hyperbolic 3-manifolds, and structure of arithmetic lattices in Lie groups. This is joint work with D. Fisher and M. Mj.
. I will report on recent progress on this question that uses ideas from infinite ergodic theory, profinite actions, representation theory, Brownian motion, random walks and the structure of locally compact groups. I will show how these combine to give information on commensurators and applications to problems in group theory, hyperbolic 3-manifolds, and structure of arithmetic lattices in Lie groups. This is joint work with D. Fisher and M. Mj.