A computer simulation (click to download)

An example of wave propagation on a string composed of two segments of different properties: the left with density_L = 1.0, velocity_L = 3.0, and the right with density_R = 4.0, velocity_R = 1.5. The arrow marks the position of the source (distance 6.5) which plucked the string at time 0. The vertical dashed line indicates the position of the junction. Both ends of the string are fixed.

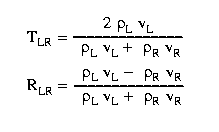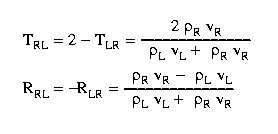The coefficients of reflection and transmission (shown above) depend not only on the string properties, but on the direction that the wave is travelling. As the wave travels from the right to the left, the density of the string decreases, and the velocity increases so that the reflection coefficient is strictly positive and the transmission coefficient is greater than 1. This means that the reflected wave will have the same sign as the incident, and that the transmitted wave will have an amplitude greater than the incident.

This animation illustrates several important facets of wave propagation:

 

When a wave encounters a fixed boundary, only a reflected pulse is generated

The polarity of the reflected pulse is opposite that of the incident pulse for a fixed boundary

When a wave encounters the middle junction, both a transmitted and a reflected pulse are generated The polarity of the reflected pulse depends on the sign of the reflection coefficient at the middle junction

When crossing the middle junction from right to left, the transmitted wave has a larger amplitude than the incident wave because the coefficient of transmission from the right to the left is greater than one. Though this effect seems counter-intuitive, it works because the total energy in the waves is a constant, rather than the amplitude of the waves.

The wavelength of a pulse changes when going across the middle junction, because the two halves have different velocities. The lower velocity on the right-hand side gives a shorter wavelength.

Finally, since this is a linear process, the waves can add both constructively and destructively. However, the waves have no lasting effect on each other; after passing through each other, they are unchanged. This idea is the basis for Fourier series methods, which represent any piecewise continuous function as a series of many harmonic waves.

 

Even though the example of the string is simple, the concepts it illustrates are used everyday by scientists and engineers. By examining seismic waves, we have learned much about the structure of the Earth. Oil and mining companies regularly use this technique to locate and exploit resources.

Download the FORTRAN source code for the frames

Download the UNIX/GMT code used to make this animation