Topological stability of actions on spheres at infinity
Abstract: The fundamental group of a negatively curved compact manifold acts by homeomorphisms on the visual boundary of its universal cover. In joint work with Jonathan Bowden, we show these actions are C^0 stable: any perturbation is a topological factor of the original action. One can do even better when the manifold is a surface and the visual sphere a circle, and along the same lines can also obtain a stronger result for actions “at infinity” of 3-manifold groups on circle that come from skew-Anosov foliations. However, in this talk, I will focus on the general rigidity result, applicable in all dimensions, and show some interesting slightly wild examples.
Slides
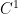 -actions on tori
-actions on tori perturbation of partially hyperbolic actions that are not smoothly conjugated to the linear one