02/08: Serge Cantat
Stationary measures on real projective surface
Abstract: Consider a real projective surface  , and a group
, and a group  acting by algebraic diffeomorphisms on
acting by algebraic diffeomorphisms on  . If
. If  is a probability measure on
is a probability measure on  , one can randomly and independently choose elements
, one can randomly and independently choose elements 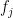 in
in  and look at the random orbits
and look at the random orbits  ,
,  ,
,  , … How do these orbits distribute on the surface? This is directly related to the classification of stationary measures on
, … How do these orbits distribute on the surface? This is directly related to the classification of stationary measures on  . I will describe recent results on this problem, all obtained in collaboration with Romain Dujardin. The main ingredients will be ergodic theory, notably the work of Brown and Rodriguez-Hertz, algebraic geometry, and complex analysis. Concrete geometric examples will be given.
. I will describe recent results on this problem, all obtained in collaboration with Romain Dujardin. The main ingredients will be ergodic theory, notably the work of Brown and Rodriguez-Hertz, algebraic geometry, and complex analysis. Concrete geometric examples will be given.