03/15: Mikolaj Fraczyk
Injectivity radius of discrete subgroups of higher rank Lie groups.
Abstract: Let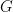 
be a simple higher rank Lie group and let 
be the associated symmetric space. Margulis conjectured that any discrete subgroup 
of 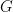such that 
has uniformly bounded injectivity radius must be a lattice. I will present the proof of this conjecture and explain how stationary random subgroups play the central role in the argument. The talk is be based on a recent joint work with Tsachik Gelander.
be a simple higher rank Lie group and let be the associated symmetric space. Margulis conjectured that any discrete subgroup of such that has uniformly bounded injectivity radius must be a lattice. I will present the proof of this conjecture and explain how stationary random subgroups play the central role in the argument. The talk is be based on a recent joint work with Tsachik Gelander.