04/12: Semyon Dyatlov

Ruelle zeta at zero for nearly hyperbolic 3-manifolds

Abstract: For a compact negatively curved Riemannian manifold $(\Sigma,g)$ , the Ruelle zeta function $\zeta_{\mathrm R}(\lambda)$ of its geodesic flow is defined for $\Re\lambda\gg 1$ as a convergent product over the periods $T_{\gamma}$ of primitive closed geodesics

$\displaystyle \zeta_{\mathrm R}(\lambda)=\prod_\gamma(1-e^{-\lambda T_{\gamma}})$

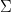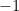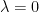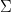and extends meromorphically to the entire complex plane. If $\Sigma$ is hyperbolic (i.e. has sectional curvature $-1$ ), then the order of vanishing $m_{\mathrm R}(0)$ of $\zeta_{\mathrm R}$ at $\lambda=0$ can be expressed in terms of the Betti numbers $b_j(\Sigma)$ . In particular, Fried proved in 1986 that when $\Sigma$ is a hyperbolic 3-manifold,

$\displaystyle m_{\mathrm R}(0)=4-2b_1(\Sigma).$

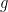I will present a recent result joint with Mihajlo Cekić, Benjamin Küster, and Gabriel Paternain: when $\dim\Sigma=3$ and $g$ is a generic perturbation of the hyperbolic metric, the order of vanishing of the Ruelle zeta function jumps, more precisely

$\displaystyle m_{\mathrm R}(0)=4-b_1(\Sigma).$

This is in contrast with dimension 2 where $m_{\mathrm R}(0)=b_1(\Sigma)-2$ for all negatively curved metrics. The proof uses the microlocal approach of expressing $m_{\mathrm R}(0)$ as an alternating sum of the dimensions of the spaces of generalized resonant Pollicott–Ruelle currents and obtains a detailed picture of these spaces both in the hyperbolic case and for its perturbations.

Slides