11/16: Jonathan DeWitt
Simultaneous Linearization of Diffeomorphisms of Isotropic Manifolds
Abstract: Suppose that 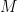 is a closed isotropic Riemannian manifold and that
is a closed isotropic Riemannian manifold and that  generate the isometry group of
generate the isometry group of 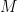 . Let
. Let  be smooth perturbations of these isometries. We show that the
be smooth perturbations of these isometries. We show that the 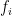 are simultaneously conjugate to isometries if and only if their associated uniform Bernoulli random walk has all Lyapunov exponents zero. This extends a linearization result of Dolgopyat and Krikorian from
are simultaneously conjugate to isometries if and only if their associated uniform Bernoulli random walk has all Lyapunov exponents zero. This extends a linearization result of Dolgopyat and Krikorian from 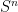 to real, complex, and quaternionic projective spaces.
to real, complex, and quaternionic projective spaces.